Vielfach hilft es schon, wenn man das, was man
weiss, anders formulieren und visualisieren kann.
Immer weniger ist es eine Frage, ob erforderliche
Daten vorhanden sind, als vielmehr, wo sie verfügbar sind und wie
sie zueinander in Beziehung gesetzt werden können.
Nicht einzelne Zahlen, sondern erst ihr Zusammenspiel und die
richtige Darstellung der Informationen schaffen die Grundlagen für
ein gemeinsames Verständnis der aktuellen Lage und der
Handlungsoptionen. Die Vektordarstellung ist eine bewährte Lösung
zur Analyse und Planung komplexer Systeme im Engineering.
Ihre Anwendung in der Organisationsentwicklung öffnet
Führungskräften auf allen Ebenen bisher undenkbare Möglichkeiten,
ihre Einsichten und neue Optionen in der Gestaltung tragfähiger
Unternehmen zu kommunizieren und umzusetzen.
Die Möglichkeiten der
Werteabbildung durch den Vektor sind so vielfältig, dass die
Beispiele hier nur einen kleinen Teil abdecken können. Versuchen
Sie diese Techniken mit Ihren eigenen Kennzahlen und machen Sie Ihre
eigenen Beispiele.
(Wenn Sie auf die Bilder klicken, erscheinen sie vergrössert.)
Sie werden entdecken, dass
Sie nach einigen (wenigen) Angewöhnungsproblemen Ihre Werte und die
Zusammenhänge der Bewertung wesentlich besser kommunizieren
können. Und dass in den Besprechungen echte Wertediskussionen
geführt werden.
|
1. Grundlagen
des Vektorprinzips für die Wertebestimmung |
|
Werte sind Eigenschaften von Objekten und
haben mehrere "Dimensionen" -
mit "objektiven" (genormten) und
"subjektiven" (von Personen abhängigen) Einheiten
(Metriken).
Mit
Vektoren ist es seit 200 Jahren in Technik und (jetzt) auch in
der Wirtschaft möglich:
-
mehrere
Werteigenschaften gleichzeitig darzustellen.
-
numerisch und auch grafisch mit mehreren
Werteigenschaften zu rechnen.
-
Werteigenschaften auch im Verbund und im
Zusammenhang eindeutiger darzustellen.
Wozu denn mehrdimensionale Werteigenschaften
visualisieren?
Um sich der "linearen" entweder-oder Argumentation
lösen zu können und mit einer "sowohl-als-auch"
Betrachtung eine wesentlich bessere Diskussions- und
Entscheidungsbasis zu haben.
|

1.1 Informationsgehalt steigt in der
Kombination |
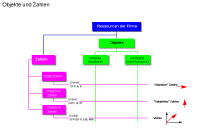
1.2 Fokus auf tangible und intangible
Ressourcen - kombiniert mit objektiven und subjektiven
Massstäben |

1.3 Entwicklung der Metriken |
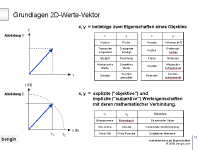
1.4 Zwei Arten von Vektoren |

1.5 Auswertungen und Vergleiche |

1.6 Auswertungen (Drill Down und
Ortskurve) |

1.7 Neun Objekte mit
jeweils zwei Werteigenschaften |
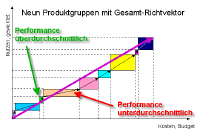
1.8 Nutzen und Kosten
|
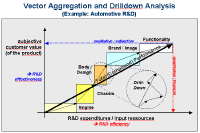
1.9 Prinzipdarstellung
(Vektoraddition und Drill Down) |
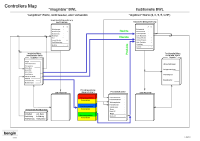
1.10 Potenziale in der imaginären
Bilanz und der imaginären Erfolgsrechnung als Voraussetzung
für monetäre Ergebnisse.
|
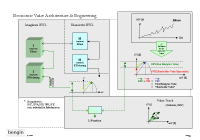
1.11 Die Verbindung der
Potenzialbilanzen mit dem Aktienkurs. |
|
|
|
|
|
2. Beispiele aus der Softwarelösung |
|
Zur Zeit haben zwei Unternehmen die Lizenz, Software zu
erstellen, mit denen Werte als Vektoren visualisiert werden.
Screen Shots der Lösungen - und Links zu weiteren
Informationen finden Sie unten.
Für neueste Informationen: software@bengin.com
|
Firma
Root Software AG
Diese Firma hat eine JAVA-Lösung entwickelt, mit der
grössere Datenmengen aus Excel - aber auch aus beliebigen
anderen Datenbanken verarbeitet werden können.
Weitere Informationen:
Firma
und Software. Download: [pdf, 900 KB]
PowerPoint
mit 11 ScreenShots des Rocsy. Download: [ppt, 1800 KB] |
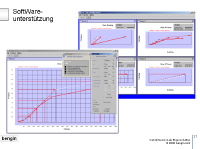
2.1 Mehrdimensionale Eigenschaften |

2.2 ScreenShots der ROCSY Lösung
|
| |
|
|
Belsoft
Informationssysteme GmbH
Die Firma Belsoft stellt seit 2006 zwei Versionen zur
Verfügung.
(A) Für Excel2003-Anwender ein Add-in (Makro) und (B) für den professionellen Einsatz eine Lösung, welche auf den
Möglichkeiten von PilotWorks www.pilotsoftware.com
aufbaut und diese erweitert.
Beispiele unter http://belsoft.bengin.com |

2.3 Drill Down mit Excel (pdf)
|

2.4 Farben bringen mehr Transparenz
|
| |
|
|
Neu seit März 2011: Für
Excel 2010
Eine Excellösung ohne Makro.
Zeigen Sie jetzt ganz einfach die
Zusammenhänge von subjektiven und objektiven Indikatoren.
Mit Excel und so einfach, wie es bisher noch nicht möglich war.
Mail an:
peter.bretscher@bengin.com
|

2.6 Drei Risiken
(als pdf) |

2.7 horizontal = Aufwand;
vertikal = subjektiver Nutzen |
| |
|
|
| 3.
Vektortyp 1 |
Bei diesem Vektortyp
können für die beiden Achsen beliebige Metriken - normierte
oder nicht-normierte - verwendet werden. Einzige Bedingung
ist, dass die einzelnen Objekte mit den gleichen Kriterien
"gemessen" werden.
Nachfolgend einige Beispiele für verschiedene monetäre und
nicht-monetäre Werte-Metriken.
Nutzen:
Durch diesen Vektortyp werden Details und Zusammenhänge nicht
mehr separat dargestellt, sonder gemeinsam. Das eröffnet
völlig neue Perspektiven in der Abbildung, der Diskussion und
der Simulation von wirtschaftlichen Realitäten.
Komplexe Prozesse werden daher eher überblickbar und
"handhabbar".
|

3.1 EFQM %-Gewicht und Umsatz
|
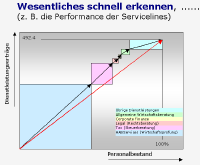
3.2 Dienstleistungserträge und
Personalbestand |
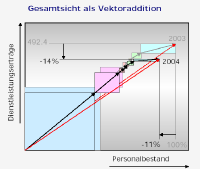
3.3 Dito mit zwei Folgejahren |
 |

3.5 Verschiedene Ressorts normiert.
Schneller Zusammenhänge
erkennen und kommunizieren.
Das Bild "übrige" zeigt hier, dass der Umsatz
schneller zurückgegangen ist, als die Mitarbeiterzahl.
|

3.6 Werteprofile einer politischen Gemeinde.
|
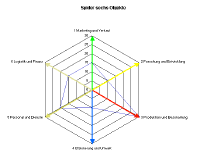
3.7 Die sechs Ressorts (gewichtet)
|
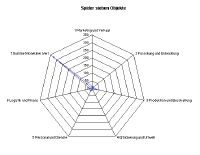
3.8 Verschiedene Budgets
|

3.9 Die sechs Ressorts:
a) einzeln und Summe
b) Gewichtung und Budget
|
|
|
|

3.10 Theoretisches Wissen Mitarbeiter |

3.11 Praktisches Können der
Mitarbeiter
|

3.12 Theoretisches und praktisches
Wissen/Können auf einen Blick |
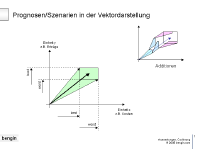
3.13 Best- und Worst-Case-
Szenarien in beiden Dimensionen |

3.14 Auswertungen Logistikbetrieb
(internal Audit) |
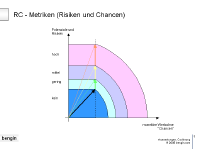
3.15 Codierung Risiken |
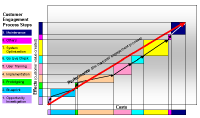
3.16 Nutzen und Kosten Software |

3.17 Lagervolumen mit Kosten
Wo wird effizienter gelagert? |

3.18 Unaxis:
Konzernergebnis und Umsatz
1995 bis 2004 (Ortskurve) |

3.19 Unaxis: EBIT und Umsatz 2002
|
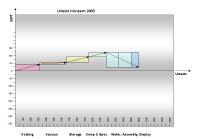
3.20 Unaxis: EBIT und Umsatz 2003 |

3.21 Unaxis: EBIT und Umsatz 2004 |

3.22 Unaxis: Investitionen in
tangible und intangible Assets 2000 bis2004 |

3.23 a) Deckungsbeitrag und Umsatz
(zum Beispiel "Budget") |

3.24 b) Deckungsbeitrag und Umsatz
("Budget" mit aktuellen Zahlen) |
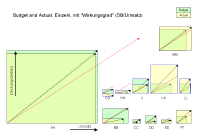
3.25 c) Budget und erreichte Zahlen
im Vergleich zur Gesamtperformance (rot) |
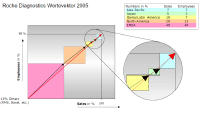
3.26 Roche Diagnostics
Zeigt die Abhängigkeiten Mitarbeiter und Verkäufe -
Vergleich von mehreren Regionen -
über-/unterdurchschnittlich?
|

3.27 Roche Pharma und Diagnostics in
den Jahren 2004 und 2005.
Zeigt die Performance (Gewinn/Umsatz) und die Entwicklung auf
einen Blick.
|
|
|
Ihre
Kombinationen?
x = ????
y = ????
|
|
4. Vektortyp
2 |
|
Hier wird die Vektorspitze über zwei
(normalerweise monetäre) Stützpunkte auf der x-Achse
bestimmt.
Zum Beispiel Kaufpreis und Herstellkosten - oder
Börsenkapitalisierung und Bilanzsumme auf der horizontalen
Achse. Durch die Umrechnung auf die y-Achse kann dann der
subjektive Wert des Käufers numerisch (und auch grafisch)
eindeutig bestimmt werden.
Dadurch ist es in den Wirtschaftslehren erstmals möglich mit
subjektiven und objektiven Werteigenschaften - Kosten und
Nutzen beispielsweise - gleichzeitig zu rechnen.
Nutzen:
Mit diesem Vektortyp wird eine mathematische Verbindung
zwischen der expliziten und der impliziten Wertachse
geschaffen.
Damit erhalten erstmals die subjektiven Werteigenschaften von
Käufern, Shareholdern, Stakeholdern.... rationale und logisch
wissenschaftliche Kennzahlen und Massstäbe, die es erlauben,
mit subjektiven Werteigenschaften zu rechnen.
Der Vektor wird dadurch zu dem idealen Instrument für die
Quantifizierung der neueren ökonomischen Entwicklungen wie
"Behavioral Economics", "Social Economy",
"Econophysics", "Hybride
Wertschöpfung".......
|

4.1 Wertschöpfung
"subjektiv" |

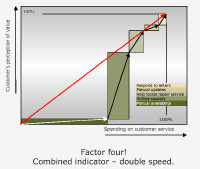
4.2 Prinzip des subjektiven
ShareholderValue
|
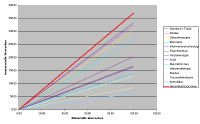
4.3 Vierzehn Branchen (Sveiby),
Bilanz und Börsenkapitalisierung
|

4.4 Immaterielle (subjektive) und
monetäre Werte von fünf Unternehmen |
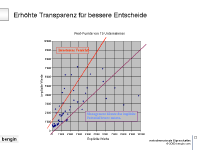
4.5 Punkte (Vektorspitzen) von 75
verschiedenen Unternehmen |

4.6 ABB (Schweiz) mit Wertschöpfung
und Kosten der Mitarbeiter |

4.7 Börsenkurve und Ortskurve
Die Ortskurve zeigt eine Veränderung bevor sie in der
Börsenkurve sichtbar wird. |

4.8 Dienstleistung: Immaterielle
Wertschöpfung beim Kunden - monetäre Wertschöpfung beim
Dienstleister.
|
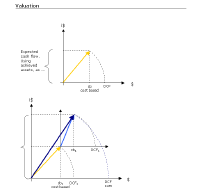
4.9 Kosten und CashFlow von zwei
Projekten (Vektoraddition) |

![]() Die
original Systeme
Die
original Systeme![]() Werte
Werte![]() Potenziale
besser nutzen
Potenziale
besser nutzen![]() Simultaneous
Engineering
Simultaneous
Engineering![]() Innovationen
Innovationen![]() Intangible
Values SwissRe
Intangible
Values SwissRe![]() Vector-Based
Performance
Vector-Based
Performance![]() HTML
Version of Vector-
HTML
Version of Vector-![]() Powerpoint
of Vector-Based
Powerpoint
of Vector-Based![]() Schumacher,
Die Philoso-
Schumacher,
Die Philoso-![]() Schumacher,
Rückkehr zum
Schumacher,
Rückkehr zum![]() Innovation
R&D (1979)
Innovation
R&D (1979)![]() Empathy Economy
Empathy Economy![]() Support Economy
Support Economy![]()
![]()




















































